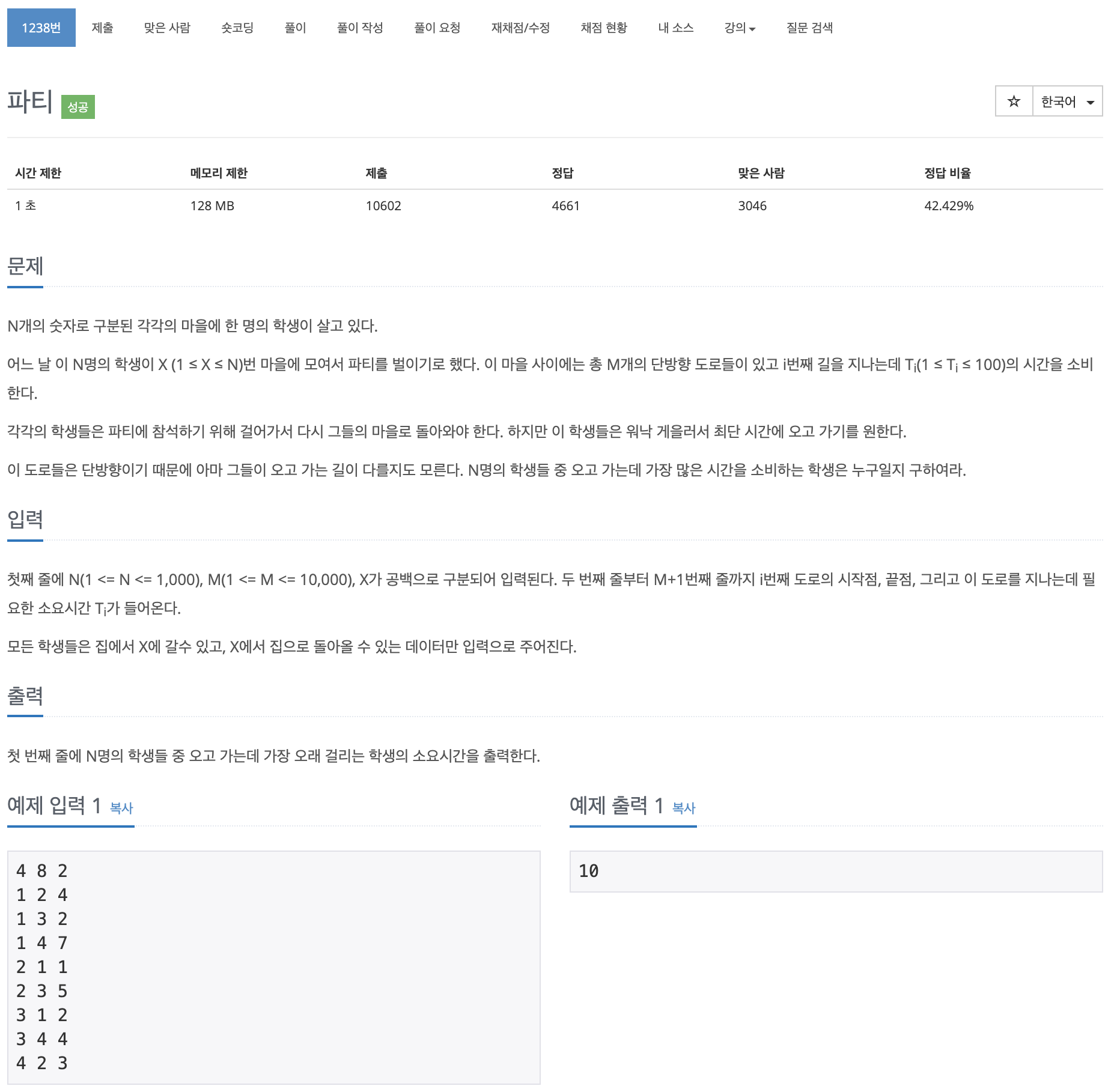
Problem
Concept & Idea
이 문제에서 가장 중요한 아이디어는 다익스트라를 두번 사용해야 한다는 점이다.
어떤 지점에서 X까지 도달하는 최소 거리 + X에서 어떤 지점까지 도달하는 최소 거리의 합의 최댓값을 구하는 문제였다.
필자는 시간초과 문제를 마주하여,, 몇 시간동안 고민했지만 바보같은 사고를 하였다.
X에서 어떤 지점까지 가는 최솟값은 두번째 다익스트라로 해결하였다.
어떤 지점에서 X까지 가는 것은 N번 돌렸었는데, X의 지점을 최대한 이용하여, 역방향 거리를 가지고 있는 벡터를 만들어서 그 벡터를 X에서 출발하면 해결할 수 있는 문제였다.
해당 테스트 케이스에서
DP1에는 4,0,6,3
DP2에는 1,0,3,7 이 들어있어서 정답 10을 구할 수 있다.
Code
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
struct node{
int x,y,z;
bool operator()(node a, node b){
return a.z>b.z;
}
};
vector<pair<int, int>> vec[1002];
vector<pair<int, int>> vec2[1002];
priority_queue<node, vector<node>, node> pqu;
int dp[1][1002],dp2[1][1002];
int main(){
int n,m,x;
scanf("%d %d %d", &n, &m, &x);
for(int i=0; i<m; i++) {
int a,b,c;
scanf("%d %d %d", &a, &b, &c);
vec[a].push_back({b,c});
vec2[b].push_back({a,c});
}
int res=-1;
for(int j=1; j<=n; j++) {
dp[0][j]=100000001;
}
dp[0][x]=0;
for(int j=0; j<vec2[x].size(); j++) {
node t;
t.x = x; t.y=vec2[x][j].first; t.z=vec2[x][j].second;
pqu.push(t);
}
while(!pqu.empty()) {
node temp = pqu.top();
pqu.pop();
if(dp[0][temp.y]>dp[0][temp.x]+temp.z) {
dp[0][temp.y]=dp[0][temp.x]+temp.z;
for(int j=0; j<vec2[temp.y].size(); j++) {
node t;
t.x = temp.y; t.y=vec2[temp.y][j].first; t.z=vec2[temp.y][j].second;
pqu.push(t);
}
}
}
for(int j=1; j<=n; j++) {
dp2[0][j]=100000001;
}
dp2[0][x]=0;
for(int j=0; j<vec[x].size(); j++) {
node t;
t.x = x; t.y=vec[x][j].first; t.z=vec[x][j].second;
pqu.push(t);
}
while(!pqu.empty()) {
node temp = pqu.top();
pqu.pop();
if(dp2[0][temp.y]>dp2[0][temp.x]+temp.z) {
dp2[0][temp.y]=dp2[0][temp.x]+temp.z;
for(int j=0; j<vec[temp.y].size(); j++) {
node t;
t.x = temp.y; t.y=vec[temp.y][j].first; t.z=vec[temp.y][j].second;
pqu.push(t);
}
}
}
for(int i=1; i<=n; i++) {
res=max(res, dp[0][i]+dp2[0][i]);
}
cout<<res<<endl;
}Fealing
다익스트라를 두 번 사용하면 된다는 생각은 잘했지만,, 한 가지 생각이 부족했다…
최소비용 만들기 문제에서는 n번 다익스트라를 돌려서 확인했기 때문에,, 이번에도 N번하면 된다고 생각했지만,, 그것이 아니었다.
그래도 다음번에는 이런 생각을 더 할 수 있지 않을까 싶다!
Check out this code in Victoria’s Gist. Please Comment my code in this link.