Vic_cinth
11049-행렬 곱셈 순서

  25 Oct 2019


Problem

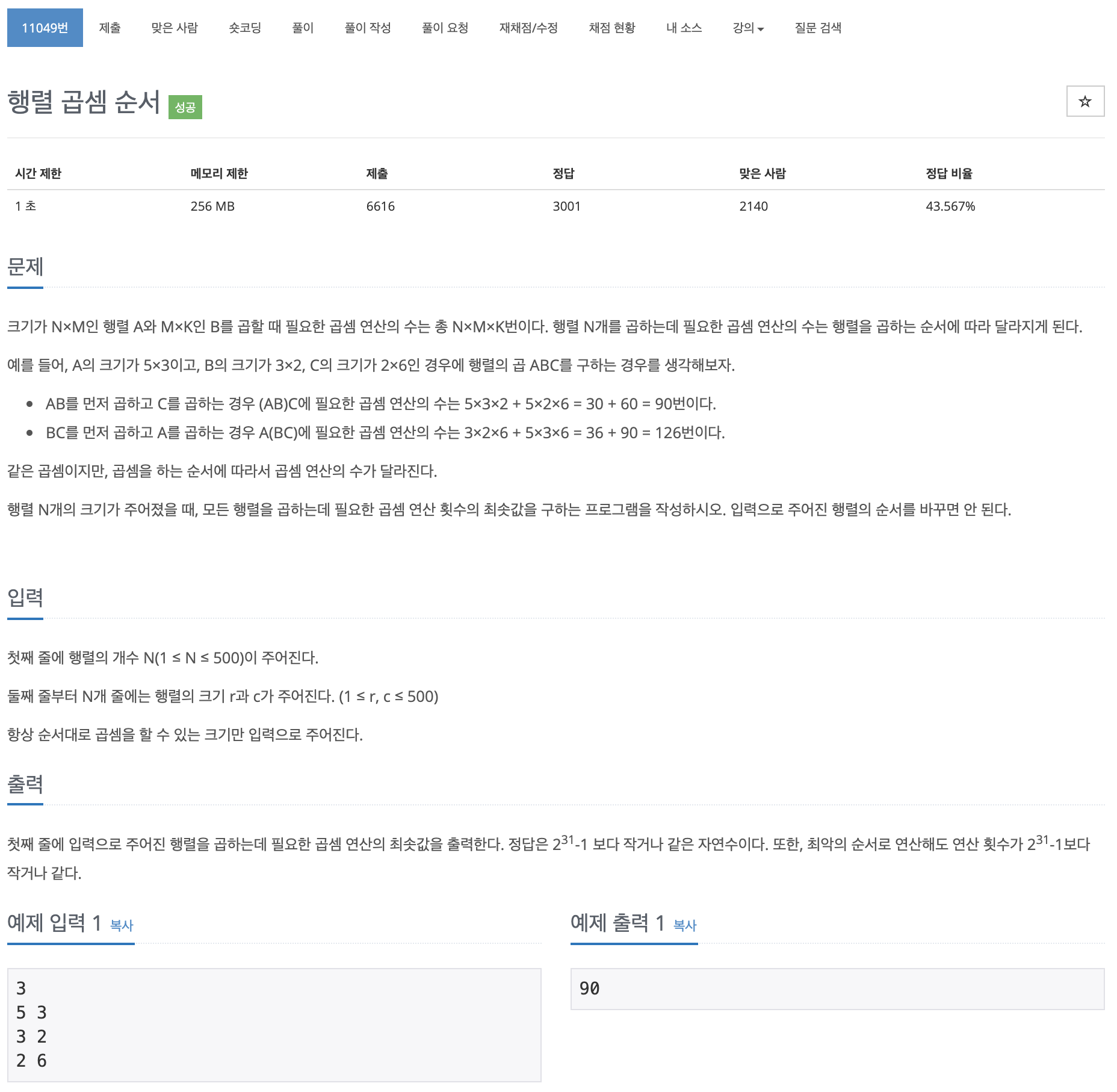
Image

Concept & Idea

가장 중요한 Concept은 DP[i][j]가 I부터 J까지의 최소 행렬 곱셉 횟수를 메모해놓는 배열이라는 점이다. 간단히 배열값을 바꿔가면서 순차적으로 검색하는 풀이는, 뒤쪽 배열들을 우선적으로 묶었을 때를 고려하지 못한다.
첫번 째 컨셉을 고려해서 문제를 풀기 시작해보자.
최종적으로 구하게되는 값은 DP[1][N]이다.
이 값을 출력하기 이전에, 계산될 과정은 DP[1][N] = DP[1][k] + DP[k+1][n] + map[1][0]map[k][1]map[n][1]; 일것이다.
Image
해당 사진처럼 인덱스를 하나하나 써가며, 풀이를 하면 필요한 작업만 연산할 수 있고, 생각의 정리를 더 잘 할 수 있게 된다.
이런 식으로 연습을 하도록 하자!

Code

#include <iostream>
using namespace std;
int n;
int map[505][2];
int dp[505][505];
#define INF 987654321
int main() {
    cin>>n;
    for(int i=1; i<=n; i++) {
        cin>>map[i][0]>>map[i][1];
    }
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++) {
            if(i!=j)
                dp[i][j]=INF;
        }
    }
    for(int i=1; i<=n; i++) {
        dp[i][i+1]=map[i][0]*map[i][1]*map[i+1][1];
    }
    for(int i=n; i>0; i--) {
        for(int j=i+1; j<=n; j++) {
            for(int k=i; k<j; k++) {
                dp[i][j]=min(dp[i][j], dp[i][k]+dp[k+1][j]+map[k+1][0]*map[j][1]*map[i][0]);
            }
        }
    }
    cout<<dp[1][n]<<endl;
}


Fealing

3일정도 이 문제로 고민했던 것 같다.
순차적으로 인덱스값을 바꿔가며, 풀었을 때는 간단한 값은 맞을 수 있었지만 생각지못했던 케이스가 있었다.
그 경우, ((AB)C)D 이런 경우는 가능하지만 (AB)(CD), A((BC)*D) 이런 경우는 고려하지 못한 풀이였다.
다이나믹 프로그래밍을 어떻게 사용해야할지, 이 풀이를 좀 더 기억해야겠다.

Check out this code in Victoria’s Gist. Please Comment my code in this link.

...